bye 08, hello 09 ;D

hours left to 2009 and i have not got myself any good resolution. haha despite to be a better guy ofcourse. hope next year will be a better year.

this year's ending party will be held at uwai's house. it'll be fun. babique. haha.

to friends, cousins. HAPPY 2009 NEW YEAR!! HOPE 09 MENJADI TAHUN YANG MENGEMBIRAKAN. haha.

and to poklen friends, hApPy nEw eR o9! hARap gEmbirA owAyz! aHaX!!


bah. n i g h t

sing with me.

sometimes late at night
i lie awake and watched her sleeping
she's lost in peaceful dreams
so i turn out the light and lay there in the dark
and the thought crosses my mind
if i never wake up in the morning
would she ever doubt the way i feel about her in my heart.

if tomorrow never comes
will she know how much i loved her
did i try in every way to show her everyday
that shes my only one
and if my time on earth were through
and she must face the world without me
is the love i gave her in the past
gonna be enough to last
if tomorrow never comes.

cause ive lost love one in my life
who never knew how much i loved them
now i left with regret
that my true feeling about them never were revealed
so i made a promise to myself
to say each day how much she means to me
and avoid the circumstance
where there's no second chance to tell her how i feel.

if tomorrow never comes
will she know how much i loved her
did i try in every way to show her everyday
that shes my only one
and if my time on earth were through
and she must face the world without me
is the love i gave her in the past
gonna be enough to last
if tomorrow never comes.

so tell that someone that you love
just what youre thinking of
if tomorrow never comes.



m o r n i n g

outing today.

woke up at 9? 10? and texted love tarus. rindu bah. haha sehari pulang baru tu. fyi, she's not around for 3 days untill sunday yakni esuk. hope she's okay. safe and sound. eisehh. haha.

2pm baru kan jalan to gadong. GADONG JUA KAN? haha. came at 2.45. sorry bro, akhir. met the acl-ians di cineplex. i thought ramai, rupanya kami around 14 saja tadi. wafiy, ampuan, shew, yayang, muiz, awie, ajik, ajib, bro lutfi, bro akif, nayeef son, myself yang known as ahmad. haha and faiz who came with us late.

overall was fun and tiring. sorry shew ah aku ambung. ngaleh bah. nanti aku layan kau saja ni. haha. muiz, nanti tani kumpul urang2 acl picnic. daripada liat wayang $4 ke $5, baik tani kumpul besemua bali ayam kan barbeque di pantai. baru best! haha. thats my plan with bro lutfi and bro akif jua kali, but i dont know you guys mau cemana. from dawn to dusk di pantai sun bathing, biar sunburn. haha apaaan. bah adangtah.

currently and officially missing my girl so badly.

hari ini.

hell o. im back lagi posting for fun, since si love has gone to her dreamland. haha.

i just got back from gadong for a family dinner, paham2 la. bonus sudaah. haha. we went to mr pizza to satisfy my brother and sisters' nafsu. haha i just ate two pieces of chicken wings and french fries. then my dad and mum went to the foodcourt to get something to eat. inda kanyang bah di mr pizza a. di foodcourt there were like thousands of peoples ratting over the places. haha. we cant hardly get a place to sit. oh btw, the other adik2 went down liat dvd kah apa. idk.

lapas we got ourself a place, my mum and me let dad order for us. but rupanya, i was the only one yang makan. malu pulang rasanya. sitting in between mum and dad who's like watching me eat. macam anak manja bah. urang lagi ramai tu. haha. lapas im full, we went home.

oh hey, its like less then an hour to 12am! you know what thats mean. haha tarih pun betukar menjadi 25 haribulan. HAPPY 7TH MONTHSARY AYANGG! ;D hope tani bekekalan seumur hidup macam tani inginkan. hehe. i love youu. love, me balum delete blog you tu. kan ambil post me yang dulu, then baru delete a. hehe.

n i g h t p e o p l e !

today.

sorry guys nada recent update lately. palui bah opera mini ku ni. almaklum lah.

today nada banyak yang berlaku untill ada text came telling ada futsal this afternoon di haruns gym. the game was against the majesty. lurus kah tu? haha. during the warm up match, we lost 6-1. kesian eh. it was half an hour match, then we make ourself about 5 teams. winner stay. my team was the first to play and win twice. first match we won by 1-0 then 6-1. the third match we lost by 2-1 kali.

i didnt manage to score any goals tadi but 'luckily' i manage to injured my lutut, dua balah punggung, and arm. haha. to acl, if ada match futsal, i wont be playing as professional as before. nayeef said injury ku any is a long term one. macam michael owen. damn jua tu. wtf! my joint arah kaki telapas. shayte. haha.

bah. n i g h t !

AcLiverchelster? wtf is that?

AcLiverchelster is a group formed by some of the wonders and their cousins on 30th November 2008. the main aim is to create a true friendship among each other by having some activities such as futsal, bowling, swimming, hang out, etc. any problem faced by any of these member are to be solved together as soon as possible.

AcLiverchelster is managed by one manager, Md Lutfi *fie* and his assistant Asrol Bahrin *srol* captain? we aint needing any captain for this group. haha. every member have their right to say something or plan something.

currently, we are having around 31 members all together;
1. Md Khairul Falah *herul*
2. Md Nayeef *ef*
3. Md Akif *chubb*
4. Abdul Al-Wafiy *fiy*
5. Iza'an Muiz *iz*
6. Izzy Syazwi *awie*
7. Haziq *ajik*
8. Najib *ajeeb*
9. Nafees *pes*
10. Haji Faiz *haji*
11. Ampuan Haziq *pam*
12. Zulkarmi *kaka*
13. Merul Esham *meyul*
14. Hassan *san*
15. Boboi *boi*
16. Nur Hisyamudien *syam*
17. Zahid *hid*
18. Md Lutfi *fie* manager
19. Asrol Bahrin *srol* assistant.
the other 12 members are the girls consist of my own love, hehe, najla, the trious, gonzales and other individual peoples. haha.

to those who are interested, do contact us. fees arent necessary but most probably we'll be making a team jersey and a hangout-uniform as what our manager planned to make. for the gent member, do prepare $30+ and as for the ladies $20 is maybe more than enough. dont ask why gents are more expensive. haha.

n i g h t !

weekend's activity.

to acliverchelster member and sesiapa sahaja yang berkaitan dengan nya, please be informed that our next activity will be held on saturday, 20th december maybe around 9? i'll be a bit early. kan joggin dulu. hee. venue: swimming pool di stadium. activiti tani swimming tu if kamu inda tau. haha duhh, 'swimming pool'. ticket is $2 for each and if youre a kind off warm hearted human, feel free to pay for me. haha a ticket plus drink and junk food will just cost you about $5? c'mon people! haha.

bring 'something' fun like ball along. siuk jua. beside eye scaning for some foxy momma. haha ehemm2. najla and her friends will be there too. soo yeaah.

JAGA KESIHATAN ANDA, SERTAI ACTIVITI KAMI IAITU BERENANG. haha wtf? lame eh.

g o o d n i g h t .

rubiks cube

The Rubik's Cube is a mechanical puzzle invented in 1974^[1] by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the "Magic Cube"^{[citation needed]}, the puzzle was licensed by Rubik to be sold by the Ideal Toys in 1980^[2] and won the German Game of the Year special award for Best Puzzle that year. It is said to be the world's best-selling toy, with over 300,000,000 Rubik's Cubes being sold worldwide by 2005.^[3]

In a classic Rubik's Cube, each of the six faces is covered by 9 stickers, among six solid colours (traditionally white, red, blue, orange, green, and yellow).^[4] A pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be a solid colour.

Conception and development

In March 1970, Larry Nichols invented a 2×2×2 "Puzzle with Pieces Rotatable in Groups" and filed a Canadian patent application for it. Nichols's cube was held together with magnets. Nichols was granted U.S. Patent 3,655,201 on April 11, 1972, two years before Rubik invented his improved cube.

On April 9, 1970, Frank Fox applied to patent his "Spherical 3×3×3". He received his UK patent (1344259) on January 16, 1974.

Rubik invented his "Magic Cube" in 1974 and obtained Hungarian patent HU170062 for the Magic Cube in 1975 but did not take out international patents. The first test batches of the product were produced in late 1977 and released to Budapest toy shops. Magic Cube was held together with interlocking plastic pieces that were less expensive to produce than the magnets in Nichols's design. In September 1979, a deal was signed with Ideal Toys to bring the Magic Cube to the Western world, and the puzzle made its international debut at the toy fairs of London, Paris, Nuremberg and New York in January and February 1980.

Packaging of Rubik's Cube, Toy of the year 1980- Ideal Toy Corp 1980, Made in Hungary.

After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western safety and packaging specifications. A lighter Cube was produced, and Ideal Toys decided to rename it. "The Gordian Knot" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980. Taking advantage of an initial shortage of Cubes, many cheap imitations appeared.

Nichols assigned his patent to his employer Moleculon Research Corp., which sued Ideal Toy Company in 1982. In 1984, Ideal lost the patent infringement suit and appealed. In 1986, the appeals court affirmed the judgment that Rubik's 2×2×2 Pocket Cube infringed Nichols's patent, but overturned the judgment on Rubik's 3×3×3 Cube.^[5]

Even while Rubik's patent application was being processed, Terutoshi Ishigi, a self-taught engineer and ironworks owner near Tokyo, filed for a Japanese patent for a nearly identical mechanism, which was granted in 1976 (Japanese patent publication JP55-008192), the 55th year of Showa era. Until 1999, when an amended Japanese patent law was enforced, Japan's patent office granted Japanese patents for non-disclosed technology within Japan without requiring worldwide novelty^[6][7]. Hence, Ishigi's patent is generally accepted as an independent reinvention at that time.^[8][9][10]

Rubik applied for another Hungarian patent on October 28, 1980, and applied for other patents. In the United States, Rubik was granted U.S. Patent 4,378,116 on March 29, 1983, for the Cube.

Around 1985, Greek inventor Panagiotis Verdes invented a method of creating cubes beyond the 5×5×5, up to 11×11×11, although he did not publish his designs at the time.^[11] Later, in 2003, he decided to file for patents, and in 2004 he received the Greek Diploma of Invention No. 1004581. As of 2008, he holds many patents in many countries for his designs. His designs include improved mechanisms for the 3×3×3, 4×4×4, and 5×5×5 which are suitable for speedcubing, whereas other existing designs for cubes larger than 5×5×5 are prone to breaking. As of June 19, 2008, the 5x5x5, 6x6x6, and 7x7x7 models are available for purchase from his online store.

The Cube celebrated its twenty-fifth anniversary in 2005, when a special edition was released, featuring a sticker in the centre of the reflective face (which replaced the white face) with a "Rubik's Cube 1980-2005" logo, and different packaging.

[edit] Mechanics

Rubik's Cube partially disassembled.

A standard cube measures 5.7 cm (approximately 2¼ inches) on each side. The puzzle consists of the twenty-six unique miniature cubes, also called "cubies" or "cubelets". However, the centre cube of each face is merely a single square façade; all are affixed to the core mechanisms. These provide structure for the other pieces to fit into and rotate around. So there are twenty-one pieces: a single core piece consisting of three intersecting axes holding the six centre squares in place but letting them rotate, and twenty smaller plastic pieces which fit into it to form the assembled puzzle. The Cube can be taken apart without much difficulty, typically by turning one side through a 45° angle and prying an edge cube away from a centre cube until it dislodges. However, as prying loose a corner cube is a good way to break off a centre cube — thus ruining the Cube — it is far safer to lever a centre cube out using a screwdriver. It is a very simple process to "solve" a Cube by taking it apart and reassembling it in a solved state. There are twelve edge pieces which show two coloured sides each, and eight corner pieces which show three colours. Each piece shows a unique colour combination, but not all combinations are present (for example, if red and orange are on opposite sides of the solved Cube, there is no edge piece with both red and orange sides). The location of these cubes relative to one another can be altered by twisting an outer third of the Cube 90°, 180° or 270°, but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered: it is fixed by the relative positions of the centre squares and the distribution of colour. However, Cubes with alternative colour arrangements also exist; for example, they might have the yellow face opposite the green, and the blue face opposite the white (with red and orange opposite faces remaining unchanged).

Douglas R. Hofstader, in the July 1982 issue of Scientific American, pointed out that Cubes could be coloured in such a way as to emphasise the corners or edges, rather than the faces as the standard colouring does; but neither of these alternative colourings has ever become popular.

[edit] Mathematics

[edit] Permutations

The original (3×3×3) Rubik's Cube has eight corners and twelve edges. There are 8! ways to arrange the corner cubes. Seven can be oriented independently, and the orientation of the eighth depends on the preceding seven, giving 3⁷ possibilities. There are 12!/2 ways to arrange the edges, since an odd permutation of the corners implies an odd permutation of the edges as well. Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 2¹¹ possibilities.^[12]

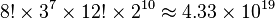
There are exactly 43,252,003,274,489,856,000 possibilities, which is approximately forty-three quintillion (short scale) or forty-three trillion (long scale). The puzzle is often advertised as having only "billions" of positions, as the larger numbers could be regarded as incomprehensible to many. To put this into perspective, if every permutation of a 57-millimeter Rubik's Cube were lined up end to end, it would stretch out approximately 261 light years. Alternatively, if laid out on the ground, this is enough to cover the earth with Rubik's cubes 275 thick.

The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times as large:

The full number is 519,024,039,293,878,272,000 or 519 quintillion (on the short scale) possible arrangements of the pieces that make up the Cube, but only one in twelve of these are actually solvable. This is because there is no sequence of moves that will swap a single pair of pieces or rotate a single corner or edge cube. Thus there are twelve possible sets of reachable configurations, sometimes called "universes" or "orbits", into which the Cube can be placed by dismantling and reassembling it.

[edit] Algorithms

In Rubik's cubists' parlance, a memorized sequence of moves that has a desired effect on the cube is called an algorithm. This terminology is derived from the mathematical use of algorithm, meaning a list of well-defined instructions for performing a task from a given initial state, through well-defined successive states, to a desired end-state. Different methods of solving the Rubik's cube each employ its own set of algorithms, together with descriptions of what the effect of the algorithm is, and when it can be used to bring the cube closer to being solved.

Most algorithms are designed to transform only a small part of the cube without scrambling other parts that have already been solved, so that they can be applied repeatedly to different parts of the cube until the whole is solved. For example, there are well-known algorithms for cycling three corners without changing the rest of the puzzle, or flipping the orientation of a pair of edges while leaving the others intact.

Some algorithms have a certain desired effect on the cube (for example, swapping two corners) but may also have the side-effect of changing other parts of the cube (such as permuting some edges). Such algorithms are often simpler than the ones without side-effects, and are employed early on in the solution when most of the puzzle has not yet been solved and the side-effects are not important. Towards the end of the solution, the more specific (and usually more complicated) algorithms are used instead, to prevent scrambling parts of the puzzle that have already been solved.

[edit] Move notation

Rubik's Cube in a scrambled state.

Rubik's Cube in solved state.

Many 3×3×3 Rubik's Cube enthusiasts use a notation developed by David Singmaster to denote a sequence of moves. This is sometimes referred to as "cube notation" or in other literature "Singmaster notation".^{[citation needed]} Its relative nature allows algorithms to be written in such a way that they can be applied regardless of which side is designated the top or how the colours are organized on a particular cube.

• F (Front): the side currently facing you
• B (Back): the side opposite the front
• U (Up): the side above or on top of the front side
• D (Down): the side opposite the top, underneath the Cube
• L (Left): the side directly to the left of the front
• R (Right): the side directly to the right of the front
• f (Front two layers): the side facing you and the corresponding middle layer
• b (Back two layers): the side opposite the front and the corresponding middle layer
• u (Up two layers) : the top side and the corresponding middle layer
• d (Down two layers) : the bottom layer and the corresponding middle layer
• l (Left two layers) : the side to the left of the front and the corresponding middle layer
• r (Right two layers) : the side to the right of the front and the corresponding middle layer
• x (rotate): rotate the Cube up
• y (rotate): rotate the Cube to the left
• z (rotate): rotate the Cube on its side to the right

When an apostrophe follows a letter, it denotes face counter-clockwise, while a letter without an apostrophe denotes a clockwise turn. Such an apostrophe mark is pronounced prime. A letter followed by a 2 (occasionally a superscript ²) denotes two turns, or an 180-degree turn.R is right side clockwise, but R' is right side counter-clockwise. The letters x, y, and z are used to indicate that the entire Cube should be turned about one of its axes. When x, y or z are primed, it is an indication that he cube must be rotated in the opposite direction. When they are squared, the cube must be rotated twice.

The 4×4×4 and larger cubes use an extended notation to refer to the additional middle layers. Generally speaking, uppercase letters (F B U D L R) refer to the outermost portions of the cube (called faces). Lowercase letters (f b u d l r) refer to the inner portions of the cube (called slices). For example: (Rr)' l2 f' means to turn the two rightmost layers counterclockwise, then the left inner layer by a half-turn, and then the inner front layer counterclockwise.

[edit] Solutions

Main article: Optimal solutions for Rubik's Cube

Wikibooks has a book on the topic of How to solve the Rubik's Cube

Although there is a significant number of possible permutations for the Rubik's Cube, there have been a number of solutions developed which allow for the cube to be solved in well under 100 moves.^{[citation needed]}

One method of solution was developed by David Singmaster and published in the book Notes on Rubik's "Magic Cube" in 1981. This solution involves solving the Cube layer by layer, in which one layer (designated the top) is solved first, followed by the middle layer, and then the final and bottom layer. After practice, solving the Cube layer by layer can be done in under one minute. Other general solutions include "corners first" methods or combinations of several other methods. In 1982, David Singmaster and Alexander Frey hypothesized that the number of moves needed to solve the Rubik's Cube, given an ideal algorithm, might be in "the low twenties". In 2007, Daniel Kunkle and Gene Cooperman used computer search methods to demonstrate that any 3×3×3 Rubik's Cube configuration can be solved in a maximum of 26 moves.^{[13] [14] [15]} In 2008, Tomas Rokicki lowered the maximum to 22 moves. ^{[16] [17] [18]}

Another common solution was developed by Jessica Fridrich. It is an efficient layer-by-layer method that employs the use of a large number of algorithms, especially for orienting and permuting the last layer.^{[citation needed]} The first-layer corners and second layer are done simultaneously, with each corner paired up with a second-layer edge piece. Fridrich's solution requires learning roughly 120 algorithms but allows the Cube to be solved in only 55 moves on average.

Philip Marshall's solution is a modified version of Fridrich's method, averaging only 65 twists yet requiring the memorization of only two algorithms^[19].

A solution developed by Ryan Heise teaches a set of underlying principles that can be used to solve the Cube in fewer than 40 moves.^{[citation needed]}

A now well-known method was developed by Lars Petrus. In this method, a 2×2×2 section is solved first, followed by a 2×2×3, and then the incorrect edges are solved using a three-move algorithm, which eliminates the need for a possible 32-move algorithm later. One of the advantages of this method is that it tends to give solutions in fewer moves. For this reason, the method is also popular for fewest move competitions.^{[citation needed]}

A number of complete solutions can also be found in some of the books listed in the bibliography.

[edit] Centre faces

The original Rubik's Cube had no orientation markings on the centre faces, although some carried the words "Rubik's Cube" on the centre square of the white face, and therefore solving it does not require any attention to orienting those faces correctly. However, if one has a marker pen, one could, for example, mark the central squares of an unscrambled Cube with four coloured marks on each edge, each corresponding to the colour of the adjacent face. Some Cubes have also been produced commercially with markings on all of the squares, such as the Lo Shu magic square or playing card suits. Thus one can nominally solve Cube yet have the markings on the centres rotated; it then becomes an additional test to solve the centers as well.

Marking the Rubik's Cube increases its difficulty because this expands its set of distinguishable possible configurations. When the Cube is unscrambled apart from the orientations of the central squares, there will always be an even number of squares requiring a quarter turn. Thus there are 4⁶/2 = 2,048 possible configurations of the centre squares in the otherwise unscrambled position, increasing the total number of possible Cube permutations from 43,252,003,274,489,856,000 (4.3×10¹⁹) to 88,580,102,706,155,225,088,000 (8.9×10²²).

[edit] Speedcubing competitions

Speedcubing (or speedsolving) is the practice of trying to solve a Rubik's Cube in the shortest time possible. There are a number of speedcubing competitions that take place around the world.

The first world championship organized by the Guinness Book of World Records was held in Munich on March 13, 1981. All Cubes were moved 40 times and lubricated with petroleum jelly. The official winner, with a record of 38 seconds, was Jury Froeschl, born in Munich. The first international world championship was held in Budapest on June 5, 1982, and was won by Minh Thai, a Vietnamese student from Los Angeles, with a time of 22.95 seconds.

Since 2003, competitions are decided by the best average (middle three of five attempts); but the single best time of all tries is also recorded. The World Cube Association maintains a history of world records ^[20]. In 2004, the WCA made it mandatory to use a special timing device called a Stackmat timer.

In addition to official competitions, informal alternative competitions have been held which invite participants to solve the Cube in unusual situations. Some such situations include:

• Blindfolded solving^[21]
• Solving the Cube with one person blindfolded and the other person saying what moves to do, known as "Team Blindfold"
• Solving the Cube underwater in a single breath^[22]
• Solving the Cube using a single hand^[23]
• Solving the Cube with one's feet^[24]

Of these informal competitions, the World Cube Association only sanctions blindfolded, one-handed, and feet solving as official competition events.^[25]

[edit] Record times

The current world record for single time on a 3x3x3 Rubik's Cube was set by Erik Akkersdijk in 2008, who had a best time of 7.08 seconds at the Czech Open 2008. He also holds the record for 4x4x4 cube.^{[citation needed]} The world record average solve is by Yu Nakajima, when he set a world record average of 11.28 seconds at the Kashiwa Open on May 4, 2008.^{[citation needed]}

[edit] Rubik's cube variations

Variations of Rubik's Cubes, clockwise from upper left: V-Cube 7, Professor's Cube, V-Cube 6, Pocket Cube, original Rubik's Cube, Rubik's Revenge.

There are different variations of Rubik's Cubes with up to seven layers: the 2×2×2 (Pocket Cube and other variants), the standard 3×3×3 cube, the 4×4×4 (Rubik's Revenge, or Master Cube), and the 5×5×5 (Professor's Cube), the 6x6x6 (V-Cube 6), and 7x7x7 (V-Cube 7).

The Cube has also inspired an entire category of similar puzzles, commonly referred to as twisty puzzles, which includes the cubes of different sizes mentioned above as well as various other geometric shapes. Some such shapes include the tetrahedron (Pyraminx), the octahedron (Skewb Diamond), the dodecahedron (Megaminx), and the icosahedron (Dogic).

[edit] Custom built puzzles

In the past, puzzles have been built resembling the Rubik's Cube or based on its inner workings. For example, a cuboid is a puzzle based off the Rubik's Cube, but with different functional dimensions, such as, 2x3x4, 3x3x5, or 2x2x4. Many cuboids are based on 4x4x4 or 5x5x5 mechanisms, via building plastic extensions or by directly modifying the mechanism itself.

Some custom puzzles are not derived from any existing mechanism, such as the Gigaminx v1.5-v2, Bevel Cube, SuperX, Toru, Rua, and 1x2x3. These puzzles usually have a set of masters 3D printed, which then are copied using molding and casting techniques to create the final puzzle.

Other Rubik's Cube modifications include cubes that have been extended or truncated to form a new shape. An example of this is the Trabjer's Octahedron, which can be built by truncating and extending portions of a regular 3x3. Most shape mods can be adapted to higher-order cubes. In the case of Tony Fisher's Rhombic Dodecahedron, there are 3x3, 4x4, 5x5, and 6x6 versions of the puzzle.

[edit] Mèffert's Puzzles

Mèffert's Puzzles is a well known distributor of twisty puzzles. Founded by Uwe Mèffert, Mèffert's Puzzles has carried many unique puzzles over the years.

Mèffert's products include the Pyramorphix, which is isomorphic with the Pocket Cube but has the shape of a tetrahedron (four of the Pocket Cube's corners have been turned into tetrahedra, the other four into flat triangles). This makes the Pyramorphix somewhat more difficult to solve than the Pocket Cube, as the isomorphism is not obvious. Mèffert has also been a long time producer of the Pyraminx, another tetrahedral twisty puzzle. More unique puzzles he has produced over the years include the Pyraminx Crystal, Impossiball, Megaminx, Skewb, and variations of the Skewb.

announcement

to everyone. especially friends and cousins.


this blog will be private by tuesday. so
please leave your blog email arah tagboard or even better, text me.

or you wont be seeing this blog again. haha. apakaaaannn.

bah, jangan nada ahh.



thank you.

meragang activities.

otw hiking and to pantai meragang.

merentasi jambatan kecik.

wafiy with his dream school. haha.

otw to pantai meragang. haha. lepak sekajap di highway.

pout from nayeef son and bro lutfi. haha.

me & bro wafiy sambil kami nungu ombak. haha apakan.

before balik from pantai, pose la sikit. haaaaaa.

nayeef son menuju puncak.



the end. good night.

love life

100% copy and paste from bro lutfi. haha. tag me if its true. hahaa. ps to love, jangan terasa aa ;p

1. King & Queen control, semua tah kan di control nya. baiktah bali kan kereta control. kan control pun sadang2 la.
2. Ice queen ( ego?) klayi bukan tah kan ngakun salahnya walaupun ya salah.
3. No chemistry. inda sefahaman. surang mau ice cream, surang mau chocolate. apakan?
4. Selingkuh? HAHAHAHAHAHA. ketahuannn!!! ani yang paling babi sekali la.
5. No freedom.semua inda buleh, tepaksa tapok2.. sabar sha.
6. Partner gauk2 tawa2 kan be cali kana signal2. kana cakapi "Bisai2 deh ulah atu!" aww sandi.
7. Permission, apa saja mesti tanya. parents nda lagi tanggung tu. bf / gf lah tanggung! haha.
8. Jalan kadai pakai baju sama jenis, sama kaler.
9. Masalah damit jadi masalah basar. macam kan durang klayi pasal tayi wah, sampai esuk2 nda betagur.
10. Ani nda semua la, Penjeles kan mati. senyum arah kawan pun inda buleh. kana tantang tarus!
11. Makan kalau sama sama paksa control, ilang skill kampung. hehehe. Ada jua yg beshare tu makan. Partnernya nda sadar tu yg partnernya sorg tu nda barus gigi apa sal gagas ngaga ia.
12. Online sampai subuh abis tu tebalik2 I love you, I miss you. mwahs.
13. When credit abis kana marah, ada tia yg cakap.. "kenapakan abis credit ah be msg sama urang lain kah?"
14. Mengusut kan mati. barang damit pun kan di kusut kan.. air liur kucing melakat arah baju pun kan menangis.
15. Sweet talker. cakap Together Forever la, janji itu ini.. baru cium bau kantut mental sudah!
16. Couple mesti kissing. HAHAHAHAHA. ada bonus. nada yang nda kissing, nda ku caya tu. Kiss tgn pipi apa, KISS jua namanya.
17. Mula mula pigang tangan ni, lama lama pigang kepala.... tuhut. Mula2 lambai lama2 bagi fuck .. sama la~
18. Kalau kelayi nda teriak2 nda sah! te sumpah sumpah. words BUDUH kuar.
19. Inda cukup sorang. mau jua ada spare.handal.
20. Kanapatan! kan menipu tapi inda handal.IQ RANDAH..HAHA. bida ehh! BOOO!!!
21. Klayi dalam keta, drive laju2. mesti di takan minyak tu! Pastu break ngajut. Plancit air liur rah cramin dapan. Cian.sawan tia bnr.
22. SARCASTIC. hehe. ada saja kan kana sindir. sabar sha laaa!
23. Inda iklas melayan pasal hari hari jumpa. Baus bah mliat dh. Mkin panjang bulu idung.
24. Handphone 24hrs di tangan. Mcm kwnku tym main bula pun pigang hp bmsn sma gfnya.handal.alum pernah hpnya gugur.main street dh tu.handal~~
25. Tukar2 line, tukar2 handphone, email swap. Rasa bah kn liat mncek sapa dangan bf/gf kuntek.Partner mana tau..mcm msn ada yg spare lagii~
26. LOVE =! CURANG
27. Need time 4 privacy (alasan untuk putus) ada lagi reason yang paling LAME BRABIS.need space, kan belajar dulu. hahaha.
28. Partner nya msg sama urang lain bukan BOYFRIEND/GIRLFRIEND buat "i miss you more than words?" hahaha. ani termasuk dalam golongan curang jua kali.. heh.
29. Inda kana bagi jadi kemarahan. WAHAHAHAA!! Selalu ni.kalau pgi2 urg masam2 muka apa grenti pasal smalam tu.assume sja..paham2 la.for fun sarapan pgi.AHAHAHA.
30. Baru 2-3 bulan together buring sudah. mau lagi yang baru. kanyang lari.
31. Kalau di tanya "handsome ka ku ni yang?" gf jawab " handsomeee ehh!! Bnr!!" tapi dalam hati (bulu idung nya tekeluar ah.)
32. Awal awal pemalu.. lama lama nda tau malu..
33. Main transfer credit.ada gi pandai bunga bunga cakap “cr me low ni..kapih lagi so masani save2 dulu bmsg” pastu ada tia kana forward kn..hahaha
34. Pengikis! hint ckp baju lawa tia, sampai partner ckp "bahh esuk balikan"
35. Couple mesti liat muvee di cinema. baru romantic ~
36. Anniversary celebrate tiap bulan. abis duit. .haha.
37. Dulu2 nda jumpa sehari kan mati rasanya, masani dh jumpa kan mati plg rasanya.
38. Awal2 mau pujuk, batah2 malas tia kan pujuk. pebaik ia menangis smpai ingus nya di lantai..
39. LELAKI, kalau ada game, bula, kereta, makanan.gitar. jadi GF pertama drg tia. Nda tia drg pedulikan gfnya.ada tia bealasan.dluar ku tdi.
40. BINI2, kalau meliat ceta KOREA handsome2 angau2 , mcm BOUTA sul drg. bf nda telayan.sanggup tu bjaga abiskn 2pack CD aa.alasan tdo..AHHAHAHAHA.lagi tia.
41. (18PL.didelete..hahaha)42. Bejalan kajap ke kadai kaling pun mesti miskol pakai loudspeaker.
43. Kalau nda kana balas miskol kana msg "behapa tu?" kana balas lagi "beria ku tdi" dahto kana tanya lagi "banar kan tu?" membari malas. hahaha.
44. Takut gf/bf inda kana suruh jalan bagi alasan TIDUR padahal bejaur. erm. Ada ni tau ku jua.
45. Partner kana balikan brg, inda pandai besyukur. mau jua yg mahal. branded. eh kira pengikis la jua..
46. Lelaki nda dapat liat bini2 hot. mcm bayi tia usul drg. mun lapar baik asak semua.
47. Bini2 kalau liat bf nya liat bini2 lain kana cubit. Kana tantang lgitu sampai2 ingus bah kuar!48. Minta ambil, akhir sikit jadi kemarahan. mau jua on time.bini2 ni biasa camni.drg aa nda sadar mun besiap aa kan mati batahnya.laki2 harum2 nunggu smpai kuar bah bau ketiak drg nunggu.
49. Kalau be SMS, ujung2 nya mesti ada words "luv u. mwahs" its a MUST.
50. Friendster, facebook mesti ada gambar berdua.
51. MSN mesti nick nya jiwang2 example : zee’s, zees’s properties.kalau nda pun ada tia nicknya drg buat bad mood la..i don’t trust u la..atu something bekenaan love life drg la tu..
52. Selalu bagi lagu macam "eh lagu ani untuk you ni dangar ahhh"
53. Bila ada urang lain.. minta putus, bila sudah putus menyasal tia kan go back. buduh!
54. Abis klayi tamparan muka. abistu ambil uleh arah urang lain. Mulut bauu.makan sampah kah kau kelmarin?hoho
55. Jumpa kawan lama buat inda kenal, kana ucap buang batu la itu ini. pasal takut kana marah. ciannn..
56. Kalau miskol kana reject kana ucap sma urang lain tym atu. hahaha.57. Da problem sikit2 minta putus.rasa bah..kes baus dah ni..
58. Sanggup online 247 tunggu partner nya online....
59. Kadang2 ada yg tipu parents rasa kn bejumpa, escape sekulah. (kalau parents alom approve) biasanya bini2 illegal ni camni.illegal means below 18.haha.
60. *kalau adakan di tambah,copy saja*

Anti-Stigma: Do You Know the Facts?

Stigma is not just a matter of using the wrong word or action. Stigma is about disrespect. It is the use of negative labels to identify a person living with mental illness. Stigma is a barrier. Fear of stigma, and the resulting discrimination, discourages individuals and their families from getting the help they need. An estimated 22 to 23 percent of the U.S. population experience a mental disorder in any given year, but almost half of these individuals do not seek treatment (U.S. Department of Health and Human Services, 2002; U.S. Surgeon General, 2001).

The educational information on this web site encourages the use of positive images to refer to people with mental illness and underscores the reality that mental illness can be successfully treated.

Do you know that an estimated 44 million Americans experience a mental disorder in any given year?

Do you know that stigma is not a matter of using the wrong word or action?

Do you know that stigma is about disrespect and using negative labels to identify a person living with mental illness?

Do you know that stigma is a barrier that discourages individuals and their families from seeking help?

Do you know that many people would rather tell employers they committed a petty crime and served time in jail, than admit to being in a psychiatric hospital?

Do you know that stigma can result in inadequate insurance coverage for mental health services?

Do you know that stigma leads to fear, mistrust, and violence against people living with mental illness and their families?

Do you know that stigma can cause families and friends to turn their backs on people with mental illness?

Do you know that stigma can prevent people from getting access to needed mental health services?

DO'S

Do use respectful language

Do emphasize abilities, not limitations.

Do tell someone if they express a stigmatizing attitude.

DONT'S

Don't portray successful persons with disabilities as super human.

Don't use generic labels such as retarded, or the mentally ill.

Don't use terms like crazy, lunatic, manic depressive, or slow functioning

transfer rumors

It’s a new week, and there’s a wealth of transfer news and rumors to run through as we get a new week started.

Manchester United in Pole Position for Benzema?

Will Manchester United be the team to beat for Karim Benzema’s signature? They just might be, but it will hinge on their decision regarding Carlos Tevez’s permanent signing.

Arsenal Still Interested in Liverpool’s Alonso

Arsenal were interested in Liverpool midfielder Xabi Alonso in the summer, and though that didn’t turn into anything, the Gunners haven’t shaken their interest in him.

Michael Owen to Chelsea?

Talk about an interesting tidbit. Could Chelsea really make a move for Michael Owen? That’s what The Sun is saying.

Juventus Like Gallas and Malouda

Juventus want to add a little more French flair to their side, oui oui. William Gallas and Florent Malouda have been linked with exits at their respective clubs, and Juve has interest in both.

Keane or Crouch for Tottenham?

The chances are pretty high that Tottenham could make a January striker for a striker who was previously on their books, whether it’s Robbie Keane or Peter Crouch.

Lazio Loan Move for Elano?

According to reports, Lazio could try to sign Manchester City’s Elano on loan in order to fill a need in midfield.

Premier League Quartet in for Pantelic?

Hertha Berlin striker Marko Pantelic is reportedly a target for Everton, Middlesbrough, West Brom, and Wigan.

todays story.

came to gadong around 2+ and met momoi, awie, asrol, and ajib di chill. then jalan2 la tawaf di gadong macam biasa. haha. *skip2* jumpa dorang bro lutfi, bro akif, nayeef son, and ampuandi luar and dorang bawa ke ahan thai kah apa. haha.

duduk2 disana, datang dua orang gadis yang bernama momoi dari dapur kah apa bersama seorang lagi gadis membawa cake sambil dorang bernyanyi. haha. i wasnt surprise pulang ;p haha. its soooo obvious guys. thank you to all. it was a great surprise. tapi yang surprise me a lot was si najla ada ah. giiiillllaaaa. the best present ever tu, guys. haha. thank you soo muchh. you all are the best EVERR. walaupun i told you yang i dont want any surprises. haha. inda ku dapat lupa kan ni.

lapas disana kami jalan ke mall. and buat planning kan jalan lagi on monday for twilight. momoi's treat tu ah. hahaa. then najlove and me jalan berdua sekajap. haha we did nothing guys. banarrr. haha. lapas atu bro wafiy came and kami balik. before atu singgah makan di JT sekajap. oh fyi, najlove ada tu with us time di kerita beside me. haha. siuk bah yo. once again, thanks again bro wafiy. banyak dusa ku ni. haha.

bah, i leave you with some picture yang tadi. enjoyy. hahaa.

im bored.

im currently listening to compromise. song from imran ajmain the singapore singer. kali. pasalnya kan si imran bin haji ma'in balum menjadi artist. haha wtf? naah liriknya. lagunya atu nanti2 tah.

love is not a given
youre not forgiven
but we all easily submit.

you have forsaken
what you have taken
so we all still incomplete.

i thought we were playing a similar game
and after these years its still been the same
and you, of all people, still have your name.

what about compromise?
i hold no disguise
you should know better.

*chorus*
its not i dont want you, i want you.
but i need you to be
a little faithful and grateful and loyal to my needs
dont think i was selfish
im selfless
and afterall ive given you
its not i dont love you
i love you
well, atleast i try to.

trust is not an object
you could reject
but we all easily believe

you have been waiting
and all ive been saying
'please be there for me'

its not like we got a thousand years
ive yet to express to you all of fears
and while you have wasted all of your tears.

what about compromise?
why do i pay the price?
only you have the answer, answer.

*chorus*

*bridge*
i know im not perfect but i deserve respect
and afterall thats said and done
you remain the only one in my heart
its not my ego
but if you go
i'd have so much to say

did we pick a good fight
to prove who's wrong and who's right?
can we finally compromise?

*chorus 2x*

can we atleast talk about it?
can we atleast compromise?

planning for the birthday boy.

N O N E ! ohh noo. mudahantah ada last minutes event karang eh. small family party sudah memadai. haha.

i would like to thanks adam who greets me yang awal tadi. he was 2minutes earlier. haha guess his watch was set wrongly. haha joke. then ampuan. andthen momoi's message came with muiz name in it. thanks guys. right after i replied those message, i tried calling si love. lapas the second time baru beangkat. where'd you go? haha we talked and talke and was disturbed by a creature name siti si aqilah. HAHA kidding. oh love greet yang ketiga. why not the first honney? hee. atleast she sang one line dari lagu birthday for me. haha. while i was on phone, asrol texted. sorry bro, inda tereply. kredit ku limited. haha nanti belanja (aku) haha. later bro lutfi, bro akif and nayeef son. thanks cousins, for the greets arah blog kamu. to the people yang kan liat the greet, just Click Hereor Click Here. if inda dapat, just click on their names arah link. lupaku apa url dorang. haha.

lapas on phone, nafees ada message. thanks bro. macam words ku kau pakai ah. haha inda apa la. i went online, using emel yang sabut ting. bro najib text time baru connect ah. haha laju kau atu bro. si flash kah? haha. nice chatting with you tadi, cousin. nanti kitani kikis si muiz ah. haha time cerita twilight. later, faiz and afiqah text. thanks guys. fiqah, jangan lupa tu ah. ice cream. yang 50 sen pun syukur tah. haha but if yang di tempat high class sikit, lagi syukur alhamdulilah tu. haha.

ada lagi yang tinggal kah? ermmm oh yeaa. badiatul or better and worst known as badil. haha a friend from ugama school greet arah nick saja. why dont you text me, girl? malu kali. haha or forgot my emel? its totally impossible. thanks anyway.

the 67s family wont be having any penyembelihan this year due to nini's health. get well soon, nini. i'll come and visit you nanti. MAYBE.

kata kata penutup dari birthday boy.
i'd lile to say thankyou to my parents, especially my mum and dad who have been supporting me from the beginning, family, friends and especialy to all my voters and fans out there! i love you guys. haha apakan? macam manang award pulang. but someday, maybe tecapai jadi the most successfull business man in brunei, atleast. haha.

so goodbye 16, and hell oo good looking 17. haha. i'd like to say thankyou to friends and cousins who helped me before. hope ani my year to help you guys balik. haha.

bah. im leaving. i'll update soon if ada something happen karang. im sleepy and love tidur kali sudah.

PS. FRUST KU SI EMEL KELUAR!! KAU PUNYA PASAL TU MUIZ! hahaa.

g o o d n i g h t

todays event.

went to kebajikan with cousins and friends just now for futsal. we came a little bit late, around 2.15 la cematu. when we arrived sana, eihh mana dorang anikan? haha. lucky dorang arrived 10 minutes lapas atu.

i have to wait for my dad. ia membawakan kasut. fyi, im still at lutfi's crib. around 2.30 baru ku main. sorry guys, i wasnt on my form tadi. i lost my golden touch right after our 1 nil win over sport school ah. haha.

but! ada but ni. my goalkeeping skill was on fire. i blocked 2501 shots tadi. haha tia karang. just before the final whistle, i couldnt save the shot from idontknowwho. fullstreched pulang sudah, its just my respond was low and kinda weak. ngaleh wah. haha.

bah eihh. im tired. goodnight. love, enjoy the concert a. dont mind me, me tidur saja.

dear diary,

i am tired and i drank too much water dari swimming pool. guess what? batuk ku hilang ulehnya ah! haha cant believe its a good, cheap and fun medicine.

im bored actualy nya ni. and waiting for her text to come. tidur kali. nada bunyi2 bah. yang ada bunyi hujan and urang tidur bekuruh. haha siapa tu ah? bro lutfi kah? cause nayeef is busy with his phonee. haha oops!

i am currently suffering
-a really bad cold. gangster type.
-inner problems called lamee.
-amai tangan. haha wtf.

ermm to muiz, im not really sure weather im coming to the futsal thingy tomorow. i didnt bring my shoe along. haha if you have extra pair, why dont you lend it to me? haha speakinnngg. nada lurus english ah.

yawwnn. goodnight. tagboard is open.

today's day out.

i woke up at 10 tadi pasal ada urang siring tadi atu bising. haha. then tarus text si love. rupanya dia lagi awal bangun. eishh. nada membangunkan a ;p

around 1.30 wafiy came menjadi transporter kami. haha. thanks bro. unfortunately, he cant join us pasal masalah tertentu. haha. we reached our destination cun2 pukul 2 and saw muiz di chill all alone with coke nya. haha. kami pun terus duduk. oh bytheway, by that time sher si adik angkat baru sampai jua. woaa long time no see si adik ah. haaa.

inda batah kemudian, awie, ajik and jeeb came. then last2 baru si anna. then kami masuk. we were plannin to watch movie, tapi inda jadi. so kami jalan2 ke archade, then rezqun 4th floor macam si talur. haha then went back tu chill.

we took some picture di chill. check out arah blog si muiz saja. haha. or better not. i look bida. haha. before 5 dorang pun balik and tinggal kami tiga, faiz, nafees, momoi and yayang.

after dorang balik, ada kami jumpa yayah (cousin balah mama) and tarus minta belanja. haha she gave us $10 and bought ourself some fundonut. haha. before 6 kami balik and the end.

tagged oleh yayang and siapa saja.

write your FULL NAME with your elbow
no backspacing
tag 10 people to do this.


Mfhd khapirul faljh bin kifle.
*atu handaaal! haha

- semua yang ada arah link ku ;D

countdown day 1.

reminder to people/readers, you have another 7days to buy me present! haha my birthday is on 8 dec if kamu inda tau and nada baca about me ku. haha.

i have not plan anything today, and tomorrow jua. if apa2, im available guys. text me if kan hang out or apasaja. wednesday, i'll be sleeping over bro lutfi's crib with nayeef, not more than a week. haha i've got to get home before my anniversary. haha apakan.

oh bytheway, i always spell center jadi centre. haha mana lurus kan? wtf juaa.

bah. update soon lagi.