
The Rubik's Cube is a mechanical puzzle invented in 1974[1] by Hungarian sculptor and professor of architecture Ernő Rubik. Originally called the "Magic Cube"[citation needed], the puzzle was licensed by Rubik to be sold by the Ideal Toys in 1980[2] and won the German Game of the Year special award for Best Puzzle that year. It is said to be the world's best-selling toy, with over 300,000,000 Rubik's Cubes being sold worldwide by 2005.[3]
In a classic Rubik's Cube, each of the six faces is covered by 9 stickers, among six solid colours (traditionally white, red, blue, orange, green, and yellow).[4] A pivot mechanism enables each face to turn independently, thus mixing up the colours. For the puzzle to be solved, each face must be a solid colour.
Conception and development
In March 1970, Larry Nichols invented a 2×2×2 "Puzzle with Pieces Rotatable in Groups" and filed a Canadian patent application for it. Nichols's cube was held together with magnets. Nichols was granted U.S. Patent 3,655,201 on April 11, 1972, two years before Rubik invented his improved cube.
On April 9, 1970, Frank Fox applied to patent his "Spherical 3×3×3". He received his UK patent (1344259) on January 16, 1974.
Rubik invented his "Magic Cube" in 1974 and obtained Hungarian patent HU170062 for the Magic Cube in 1975 but did not take out international patents. The first test batches of the product were produced in late 1977 and released to Budapest toy shops. Magic Cube was held together with interlocking plastic pieces that were less expensive to produce than the magnets in Nichols's design. In September 1979, a deal was signed with Ideal Toys to bring the Magic Cube to the Western world, and the puzzle made its international debut at the toy fairs of London, Paris, Nuremberg and New York in January and February 1980.
After its international debut, the progress of the Cube towards the toy shop shelves of the West was briefly halted so that it could be manufactured to Western safety and packaging specifications. A lighter Cube was produced, and Ideal Toys decided to rename it. "The Gordian Knot" and "Inca Gold" were considered, but the company finally decided on "Rubik's Cube", and the first batch was exported from Hungary in May 1980. Taking advantage of an initial shortage of Cubes, many cheap imitations appeared.
Nichols assigned his patent to his employer Moleculon Research Corp., which sued Ideal Toy Company in 1982. In 1984, Ideal lost the patent infringement suit and appealed. In 1986, the appeals court affirmed the judgment that Rubik's 2×2×2 Pocket Cube infringed Nichols's patent, but overturned the judgment on Rubik's 3×3×3 Cube.[5]
Even while Rubik's patent application was being processed, Terutoshi Ishigi, a self-taught engineer and ironworks owner near Tokyo, filed for a Japanese patent for a nearly identical mechanism, which was granted in 1976 (Japanese patent publication JP55-008192), the 55th year of Showa era. Until 1999, when an amended Japanese patent law was enforced, Japan's patent office granted Japanese patents for non-disclosed technology within Japan without requiring worldwide novelty[6][7]. Hence, Ishigi's patent is generally accepted as an independent reinvention at that time.[8][9][10]
Rubik applied for another Hungarian patent on October 28, 1980, and applied for other patents. In the United States, Rubik was granted U.S. Patent 4,378,116 on March 29, 1983, for the Cube.
Around 1985, Greek inventor Panagiotis Verdes invented a method of creating cubes beyond the 5×5×5, up to 11×11×11, although he did not publish his designs at the time.[11] Later, in 2003, he decided to file for patents, and in 2004 he received the Greek Diploma of Invention No. 1004581. As of 2008, he holds many patents in many countries for his designs. His designs include improved mechanisms for the 3×3×3, 4×4×4, and 5×5×5 which are suitable for speedcubing, whereas other existing designs for cubes larger than 5×5×5 are prone to breaking. As of June 19, 2008, the 5x5x5, 6x6x6, and 7x7x7 models are available for purchase from his online store.
The Cube celebrated its twenty-fifth anniversary in 2005, when a special edition was released, featuring a sticker in the centre of the reflective face (which replaced the white face) with a "Rubik's Cube 1980-2005" logo, and different packaging.
[edit] Mechanics
A standard cube measures 5.7 cm (approximately 2¼ inches) on each side. The puzzle consists of the twenty-six unique miniature cubes, also called "cubies" or "cubelets". However, the centre cube of each face is merely a single square façade; all are affixed to the core mechanisms. These provide structure for the other pieces to fit into and rotate around. So there are twenty-one pieces: a single core piece consisting of three intersecting axes holding the six centre squares in place but letting them rotate, and twenty smaller plastic pieces which fit into it to form the assembled puzzle. The Cube can be taken apart without much difficulty, typically by turning one side through a 45° angle and prying an edge cube away from a centre cube until it dislodges. However, as prying loose a corner cube is a good way to break off a centre cube — thus ruining the Cube — it is far safer to lever a centre cube out using a screwdriver. It is a very simple process to "solve" a Cube by taking it apart and reassembling it in a solved state. There are twelve edge pieces which show two coloured sides each, and eight corner pieces which show three colours. Each piece shows a unique colour combination, but not all combinations are present (for example, if red and orange are on opposite sides of the solved Cube, there is no edge piece with both red and orange sides). The location of these cubes relative to one another can be altered by twisting an outer third of the Cube 90°, 180° or 270°, but the location of the coloured sides relative to one another in the completed state of the puzzle cannot be altered: it is fixed by the relative positions of the centre squares and the distribution of colour. However, Cubes with alternative colour arrangements also exist; for example, they might have the yellow face opposite the green, and the blue face opposite the white (with red and orange opposite faces remaining unchanged).
Douglas R. Hofstader, in the July 1982 issue of Scientific American, pointed out that Cubes could be coloured in such a way as to emphasise the corners or edges, rather than the faces as the standard colouring does; but neither of these alternative colourings has ever become popular.
[edit] Mathematics
[edit] Permutations
The original (3×3×3) Rubik's Cube has eight corners and twelve edges. There are 8! ways to arrange the corner cubes. Seven can be oriented independently, and the orientation of the eighth depends on the preceding seven, giving 37 possibilities. There are 12!/2 ways to arrange the edges, since an odd permutation of the corners implies an odd permutation of the edges as well. Eleven edges can be flipped independently, with the flip of the twelfth depending on the preceding ones, giving 211 possibilities.[12]
There are exactly 43,252,003,274,489,856,000 possibilities, which is approximately forty-three quintillion (short scale) or forty-three trillion (long scale). The puzzle is often advertised as having only "billions" of positions, as the larger numbers could be regarded as incomprehensible to many. To put this into perspective, if every permutation of a 57-millimeter Rubik's Cube were lined up end to end, it would stretch out approximately 261 light years. Alternatively, if laid out on the ground, this is enough to cover the earth with Rubik's cubes 275 thick.
The preceding figure is limited to permutations that can be reached solely by turning the sides of the cube. If one considers permutations reached through disassembly of the cube, the number becomes twelve times as large:
The full number is 519,024,039,293,878,272,000 or 519 quintillion (on the short scale) possible arrangements of the pieces that make up the Cube, but only one in twelve of these are actually solvable. This is because there is no sequence of moves that will swap a single pair of pieces or rotate a single corner or edge cube. Thus there are twelve possible sets of reachable configurations, sometimes called "universes" or "orbits", into which the Cube can be placed by dismantling and reassembling it.
[edit] Algorithms
In Rubik's cubists' parlance, a memorized sequence of moves that has a desired effect on the cube is called an algorithm. This terminology is derived from the mathematical use of algorithm, meaning a list of well-defined instructions for performing a task from a given initial state, through well-defined successive states, to a desired end-state. Different methods of solving the Rubik's cube each employ its own set of algorithms, together with descriptions of what the effect of the algorithm is, and when it can be used to bring the cube closer to being solved.
Most algorithms are designed to transform only a small part of the cube without scrambling other parts that have already been solved, so that they can be applied repeatedly to different parts of the cube until the whole is solved. For example, there are well-known algorithms for cycling three corners without changing the rest of the puzzle, or flipping the orientation of a pair of edges while leaving the others intact.
Some algorithms have a certain desired effect on the cube (for example, swapping two corners) but may also have the side-effect of changing other parts of the cube (such as permuting some edges). Such algorithms are often simpler than the ones without side-effects, and are employed early on in the solution when most of the puzzle has not yet been solved and the side-effects are not important. Towards the end of the solution, the more specific (and usually more complicated) algorithms are used instead, to prevent scrambling parts of the puzzle that have already been solved.
[edit] Move notation
Many 3×3×3 Rubik's Cube enthusiasts use a notation developed by David Singmaster to denote a sequence of moves. This is sometimes referred to as "cube notation" or in other literature "Singmaster notation".[citation needed] Its relative nature allows algorithms to be written in such a way that they can be applied regardless of which side is designated the top or how the colours are organized on a particular cube.
- F (Front): the side currently facing you
- B (Back): the side opposite the front
- U (Up): the side above or on top of the front side
- D (Down): the side opposite the top, underneath the Cube
- L (Left): the side directly to the left of the front
- R (Right): the side directly to the right of the front
- f (Front two layers): the side facing you and the corresponding middle layer
- b (Back two layers): the side opposite the front and the corresponding middle layer
- u (Up two layers) : the top side and the corresponding middle layer
- d (Down two layers) : the bottom layer and the corresponding middle layer
- l (Left two layers) : the side to the left of the front and the corresponding middle layer
- r (Right two layers) : the side to the right of the front and the corresponding middle layer
- x (rotate): rotate the Cube up
- y (rotate): rotate the Cube to the left
- z (rotate): rotate the Cube on its side to the right
When an apostrophe follows a letter, it denotes face counter-clockwise, while a letter without an apostrophe denotes a clockwise turn. Such an apostrophe mark is pronounced prime. A letter followed by a 2 (occasionally a superscript ²) denotes two turns, or an 180-degree turn.R is right side clockwise, but R' is right side counter-clockwise. The letters x, y, and z are used to indicate that the entire Cube should be turned about one of its axes. When x, y or z are primed, it is an indication that he cube must be rotated in the opposite direction. When they are squared, the cube must be rotated twice.
The 4×4×4 and larger cubes use an extended notation to refer to the additional middle layers. Generally speaking, uppercase letters (F B U D L R) refer to the outermost portions of the cube (called faces). Lowercase letters (f b u d l r) refer to the inner portions of the cube (called slices). For example: (Rr)' l2 f' means to turn the two rightmost layers counterclockwise, then the left inner layer by a half-turn, and then the inner front layer counterclockwise.
[edit] Solutions
 | Wikibooks has a book on the topic of |
Although there is a significant number of possible permutations for the Rubik's Cube, there have been a number of solutions developed which allow for the cube to be solved in well under 100 moves.[citation needed]
One method of solution was developed by David Singmaster and published in the book Notes on Rubik's "Magic Cube" in 1981. This solution involves solving the Cube layer by layer, in which one layer (designated the top) is solved first, followed by the middle layer, and then the final and bottom layer. After practice, solving the Cube layer by layer can be done in under one minute. Other general solutions include "corners first" methods or combinations of several other methods. In 1982, David Singmaster and Alexander Frey hypothesized that the number of moves needed to solve the Rubik's Cube, given an ideal algorithm, might be in "the low twenties". In 2007, Daniel Kunkle and Gene Cooperman used computer search methods to demonstrate that any 3×3×3 Rubik's Cube configuration can be solved in a maximum of 26 moves.[13] [14] [15] In 2008, Tomas Rokicki lowered the maximum to 22 moves. [16] [17] [18]
Another common solution was developed by Jessica Fridrich. It is an efficient layer-by-layer method that employs the use of a large number of algorithms, especially for orienting and permuting the last layer.[citation needed] The first-layer corners and second layer are done simultaneously, with each corner paired up with a second-layer edge piece. Fridrich's solution requires learning roughly 120 algorithms but allows the Cube to be solved in only 55 moves on average.
Philip Marshall's solution is a modified version of Fridrich's method, averaging only 65 twists yet requiring the memorization of only two algorithms[19].
A solution developed by Ryan Heise teaches a set of underlying principles that can be used to solve the Cube in fewer than 40 moves.[citation needed]
A now well-known method was developed by Lars Petrus. In this method, a 2×2×2 section is solved first, followed by a 2×2×3, and then the incorrect edges are solved using a three-move algorithm, which eliminates the need for a possible 32-move algorithm later. One of the advantages of this method is that it tends to give solutions in fewer moves. For this reason, the method is also popular for fewest move competitions.[citation needed]
A number of complete solutions can also be found in some of the books listed in the bibliography.
[edit] Centre faces
The original Rubik's Cube had no orientation markings on the centre faces, although some carried the words "Rubik's Cube" on the centre square of the white face, and therefore solving it does not require any attention to orienting those faces correctly. However, if one has a marker pen, one could, for example, mark the central squares of an unscrambled Cube with four coloured marks on each edge, each corresponding to the colour of the adjacent face. Some Cubes have also been produced commercially with markings on all of the squares, such as the Lo Shu magic square or playing card suits. Thus one can nominally solve Cube yet have the markings on the centres rotated; it then becomes an additional test to solve the centers as well.
Marking the Rubik's Cube increases its difficulty because this expands its set of distinguishable possible configurations. When the Cube is unscrambled apart from the orientations of the central squares, there will always be an even number of squares requiring a quarter turn. Thus there are 46/2 = 2,048 possible configurations of the centre squares in the otherwise unscrambled position, increasing the total number of possible Cube permutations from 43,252,003,274,489,856,000 (4.3×1019) to 88,580,102,706,155,225,088,000 (8.9×1022).
[edit] Speedcubing competitions
Speedcubing (or speedsolving) is the practice of trying to solve a Rubik's Cube in the shortest time possible. There are a number of speedcubing competitions that take place around the world.
The first world championship organized by the Guinness Book of World Records was held in Munich on March 13, 1981. All Cubes were moved 40 times and lubricated with petroleum jelly. The official winner, with a record of 38 seconds, was Jury Froeschl, born in Munich. The first international world championship was held in Budapest on June 5, 1982, and was won by Minh Thai, a Vietnamese student from Los Angeles, with a time of 22.95 seconds.
Since 2003, competitions are decided by the best average (middle three of five attempts); but the single best time of all tries is also recorded. The World Cube Association maintains a history of world records [20]. In 2004, the WCA made it mandatory to use a special timing device called a Stackmat timer.
In addition to official competitions, informal alternative competitions have been held which invite participants to solve the Cube in unusual situations. Some such situations include:
- Blindfolded solving[21]
- Solving the Cube with one person blindfolded and the other person saying what moves to do, known as "Team Blindfold"
- Solving the Cube underwater in a single breath[22]
- Solving the Cube using a single hand[23]
- Solving the Cube with one's feet[24]
Of these informal competitions, the World Cube Association only sanctions blindfolded, one-handed, and feet solving as official competition events.[25]
[edit] Record times
The current world record for single time on a 3x3x3 Rubik's Cube was set by Erik Akkersdijk in 2008, who had a best time of 7.08 seconds at the Czech Open 2008. He also holds the record for 4x4x4 cube.[citation needed] The world record average solve is by Yu Nakajima, when he set a world record average of 11.28 seconds at the Kashiwa Open on May 4, 2008.[citation needed]
[edit] Rubik's cube variations

There are different variations of Rubik's Cubes with up to seven layers: the 2×2×2 (Pocket Cube and other variants), the standard 3×3×3 cube, the 4×4×4 (Rubik's Revenge, or Master Cube), and the 5×5×5 (Professor's Cube), the 6x6x6 (V-Cube 6), and 7x7x7 (V-Cube 7).
The Cube has also inspired an entire category of similar puzzles, commonly referred to as twisty puzzles, which includes the cubes of different sizes mentioned above as well as various other geometric shapes. Some such shapes include the tetrahedron (Pyraminx), the octahedron (Skewb Diamond), the dodecahedron (Megaminx), and the icosahedron (Dogic).
[edit] Custom built puzzles
In the past, puzzles have been built resembling the Rubik's Cube or based on its inner workings. For example, a cuboid is a puzzle based off the Rubik's Cube, but with different functional dimensions, such as, 2x3x4, 3x3x5, or 2x2x4. Many cuboids are based on 4x4x4 or 5x5x5 mechanisms, via building plastic extensions or by directly modifying the mechanism itself.
Some custom puzzles are not derived from any existing mechanism, such as the Gigaminx v1.5-v2, Bevel Cube, SuperX, Toru, Rua, and 1x2x3. These puzzles usually have a set of masters 3D printed, which then are copied using molding and casting techniques to create the final puzzle.
Other Rubik's Cube modifications include cubes that have been extended or truncated to form a new shape. An example of this is the Trabjer's Octahedron, which can be built by truncating and extending portions of a regular 3x3. Most shape mods can be adapted to higher-order cubes. In the case of Tony Fisher's Rhombic Dodecahedron, there are 3x3, 4x4, 5x5, and 6x6 versions of the puzzle.
[edit] Mèffert's Puzzles
Mèffert's Puzzles is a well known distributor of twisty puzzles. Founded by Uwe Mèffert, Mèffert's Puzzles has carried many unique puzzles over the years.
Mèffert's products include the Pyramorphix, which is isomorphic with the Pocket Cube but has the shape of a tetrahedron (four of the Pocket Cube's corners have been turned into tetrahedra, the other four into flat triangles). This makes the Pyramorphix somewhat more difficult to solve than the Pocket Cube, as the isomorphism is not obvious. Mèffert has also been a long time producer of the Pyraminx, another tetrahedral twisty puzzle. More unique puzzles he has produced over the years include the Pyraminx Crystal, Impossiball, Megaminx, Skewb, and variations of the Skewb.


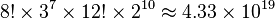



No comments:
Post a Comment